High/Low Point Search

Type: Interactive addition for various insert applications

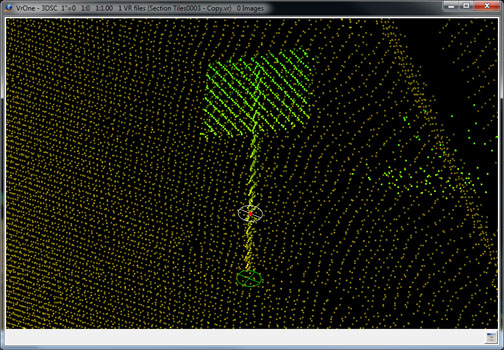
High/Low point searching is an addition to various insert applications such as Insert Line (InsLin) and Insert Symbol (InsSym). It selects the highest, lowest or mean elevation point from a group of VrPoints within a user defined radius of the point digitized.  The points considered for selection are VrPoints (LiDAR) only.  Options include the ability to use the elevation and/or the XY position of the found point and copy these coordinates as the current digitized position.  High/Low Point Search may be turned on or off at any time.

This digitizing assistant is useful when placing features such as poles, posts, and single trees. It is also useful when placing line items such as the tops of curbs and fence lines.

Parameters

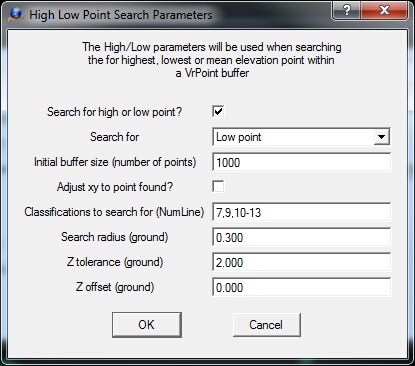
High/Low Point Search Parameters dialog

Search for high or low point?

Turns on/off high, mean or low point searching.

Search for

Specifies the search mode.  Options are Low point, Mean point or High point.

Initial buffer size (number of points)

Each time a point is digitized, VrPoints that meet the search criteria are buffered before the high, mean or low point is selected.  This parameter defines the initial buffer size in number of points.  The buffer size is dynamic and will be made larger by this parameter as often as needed.  The number of points in the buffer will be displayed in the console window each time a point is digitized.

Adjust xy to point found?

Specifies whether the X,Y position of the found VrPoint should be copied to the digitized point. This is useful if digitizing features such as hydro-graphic lines and the tops of items like fence lines.

Classification to search (Num Line)

Defines the VrPoint classifications to search when locating the high, mean or low VrPoint.  This parameter is entered as a Number Line.

Search radius (ground)

Defines the radius in ground units of the digitized point within which which VrPoints are considered.

Z tolerance (ground)

Defines the elevation range in ground units above and below the digitized point for which VrPoints are considered.  This is useful when data at other elevations might interfere with the high-low process.

Z offset (ground)

Defines the Z offset to add to the resulting high, mean or low elevation.  For example, the base of a fence could be digitized and a line added near the top.

Local Commands

The following commands will condition High/Low Point Search and may be keyed in any time it is active.  Normally, these key-ins are placed in the Local Arguments field in a Function Key to set conditions when a key is started.